Linear regression quantifies the relationship between one or more predictor variable and one outcome variable.
Regression analysis is used in determining the strength of predictors, forecasting an effect, and show the trend forecasting.
Formula to calculate linear regression.
The lines equation is as follows;

- Y – is the dependent variable.
- X – is the independent also known as explanatory variable.
- a – is the intercept.
- b – is the slope.
a and b can be calculated using the following formula.
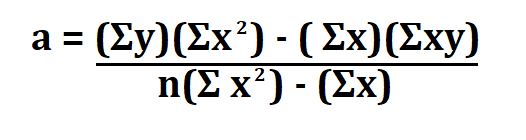
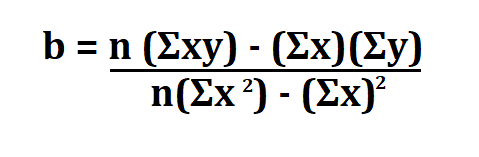
n is the sample size.
Example:
Suppose your sample size (n) is 5 and the value of Calculate Linear Regression Equation. ΣY and ΣX is 20 and 24 respectively, what will be the linear regression equation.
We will begin by calculating for a and then b.
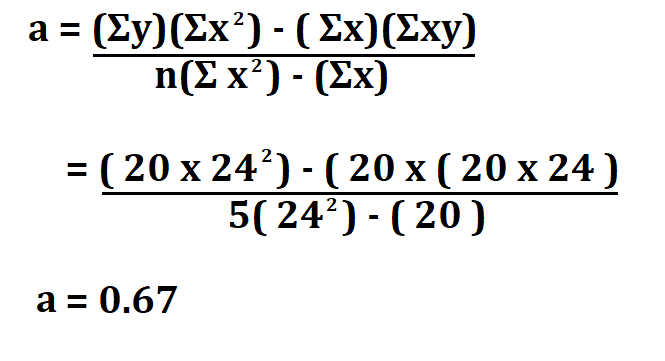
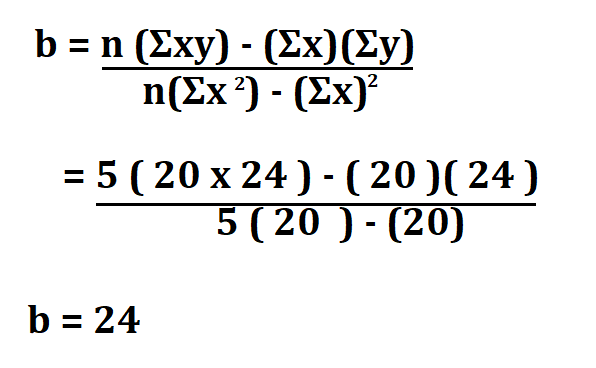
If we substitute our values of X and Y in the equation Y = a + bX we get;
Y = 0.67 + 24y