Standard deviation is a measure of how close the numbers are to the mean. It is calculated as the square root of the variance and denoted by σ (the Greek letter sigma).
Formula to calculate standard deviation.
To calculate standard deviation;
- Find the mean of the (μ) numbers given.
- Subtract the mean from each of the numbers (x), square the difference and find their sum.
- Divide the result by the total number of observations (N) and finally find the square root of the result.
Formula to determine standard deviation.
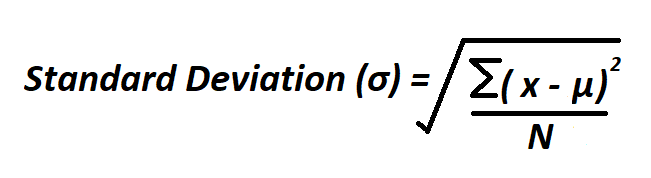
Example:
Find the standard deviation of the following numbers.
2, 4, 5, 8, 1.
We start by finding the mean of the list of data.
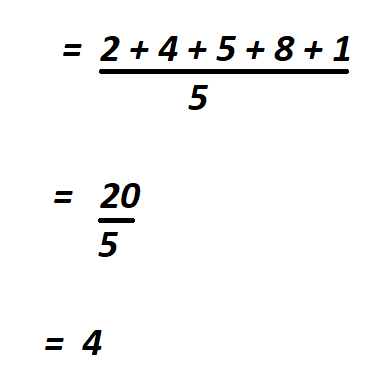
Then subtract the mean from each of the numbers, square the difference and find their sum.
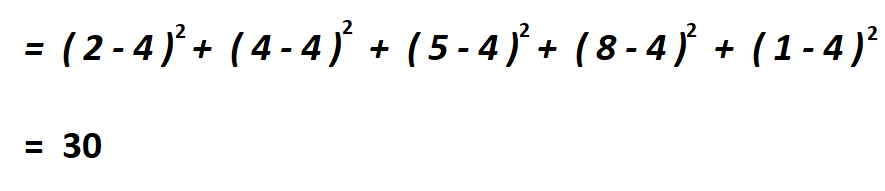
Divide the result by the total number of observations and finally find the square root of the result.
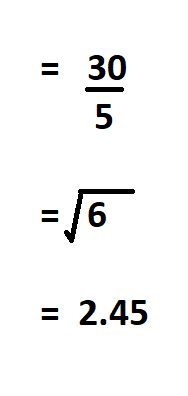
Therefore, the standard deviation of the list of data is 2.45.